10 Ml Graduated Cylinder Uncertainty

one.5: Measurement Uncertainty, Accurateness, and Precision

1. Last updated

2. Save equally PDF

Folio ID

105539

Skills to Develop

• Define accuracy and precision
• Distinguish exact and uncertain numbers
• Correctly represent dubiousness in quantities using pregnant figures
• Utilize proper rounding rules to computed quantities

Counting is the only type of measurement that is free from uncertainty, provided the number of objects beingness counted does non modify while the counting process is underway. The result of such a counting measurement is an instance of an verbal number. If we count eggs in a carton, we know exactly how many eggs the carton contains. The numbers of defined quantities are besides exact. By definition, one foot is exactly 12 inches, ane inch is exactly two.54 centimeters, and 1 gram is exactly 0.001 kilogram. Quantities derived from measurements other than counting, even so, are uncertain to varying extents due to practical limitations of the measurement process used.

Meaning Figures in Measurement

The numbers of measured quantities, unlike divers or directly counted quantities, are non exact. To measure out the book of liquid in a graduated cylinder, y'all should make a reading at the bottom of the meniscus, the lowest indicate on the curved surface of the liquid.

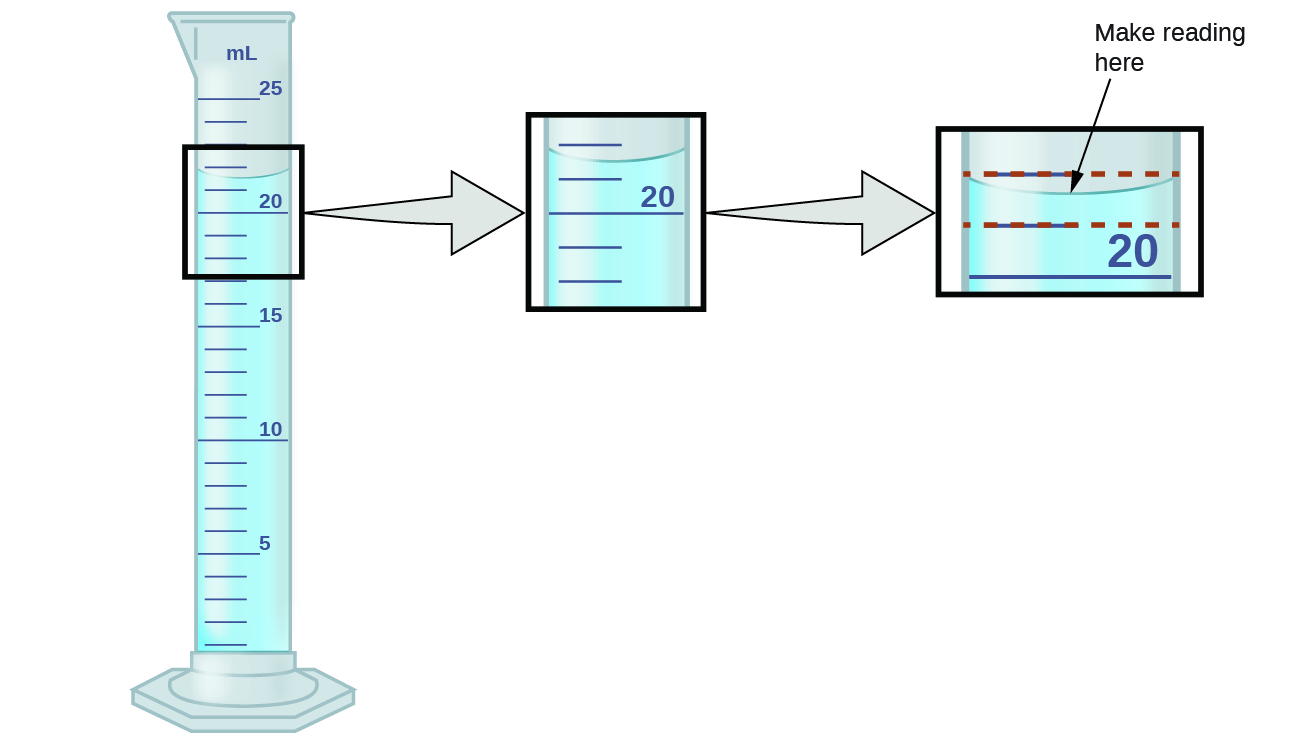
Figure \(\PageIndex{1}\): To measure the volume of liquid in this graduated cylinder, you must mentally subdivide the distance between the 21 and 22 mL marks into tenths of a milliliter, and so make a reading (estimate) at the bottom of the meniscus.

Refer to the illustration in Figure \(\PageIndex{1}\). The lesser of the meniscus in this case conspicuously lies betwixt the 21 and 22 markings, meaning the liquid volume is certainly greater than 21 mL but less than 22 mL. The meniscus appears to be a bit closer to the 22-mL mark than to the 21-mL mark, and then a reasonable gauge of the liquid's volume would be 21.six mL. In the number 21.vi, so, the digits 2 and 1 are sure, just the 6 is an estimate. Some people might estimate the meniscus position to be every bit distant from each of the markings and guess the tenth-place digit every bit 5, while others may think it to be even closer to the 22-mL mark and estimate this digit to be 7. Annotation that it would be pointless to attempt to approximate a digit for the hundredths place, given that the tenths-identify digit is uncertain. In full general, numerical scales such as the one on this graduated cylinder will allow measurements to one-tenth of the smallest calibration division. The calibration in this example has one-mL divisions, and so volumes may exist measured to the nearest 0.1 mL.

This concept holds true for all measurements, even if y'all exercise not actively make an gauge. If you place a quarter on a standard electronic balance, you may obtain a reading of 6.72 g. The digits vi and 7 are certain, and the two indicates that the mass of the quarter is likely between half dozen.71 and 6.73 grams. The quarter weighs about 6.72 grams, with a nominal doubt in the measurement of ± 0.01 gram. If we weigh the quarter on a more sensitive residual, we may find that its mass is six.723 grand. This ways its mass lies between 6.722 and 6.724 grams, an uncertainty of 0.001 gram. Every measurement has some uncertainty, which depends on the device used (and the user's power). All of the digits in a measurement, including the uncertain last digit, are called significant figures or pregnant digits. Note that nothing may be a measured value; for example, if yous stand up on a calibration that shows weight to the nearest pound and it shows "120," so the 1 (hundreds), 2 (tens) and 0 (ones) are all significant (measured) values.

Whenever you make a measurement properly, all the digits in the result are significant. But what if yous were analyzing a reported value and trying to determine what is pregnant and what is not? Well, for starters, all nonzero digits are significant, and information technology is just zeros that require some idea. Nosotros volition use the terms "leading," "trailing," and "captive" for the zeros and will consider how to deal with them.

Starting with the offset nonzero digit on the left, count this digit and all remaining digits to the right. This is the number of pregnant figures in the measurement unless the last digit is a trailing zero lying to the left of the decimal point.

Captive zeros result from measurement and are therefore always pregnant. Leading zeros, however, are never meaning—they merely tell us where the decimal point is located.

The leading zeros in this example are not significant. We could employ exponential notation (as described in Appendix B) and express the number every bit viii.32407 \(\times\) x⁻³; and so the number 8.32407 contains all of the significant figures, and 10⁻³ locates the decimal betoken.

The number of significant figures is uncertain in a number that ends with a nada to the left of the decimal indicate location. The zeros in the measurement 1,300 grams could be significant or they could simply indicate where the decimal point is located. The ambiguity can be resolved with the use of exponential annotation: 1.three \(\times\) ten³ (two significant figures), one.xxx \(\times\) 10³ (3 meaning figures, if the tens place was measured), or ane.300 \(\times\) 10³ (4 meaning figures, if the ones place was likewise measured). In cases where only the decimal-formatted number is available, it is prudent to assume that all trailing zeros are not significant.

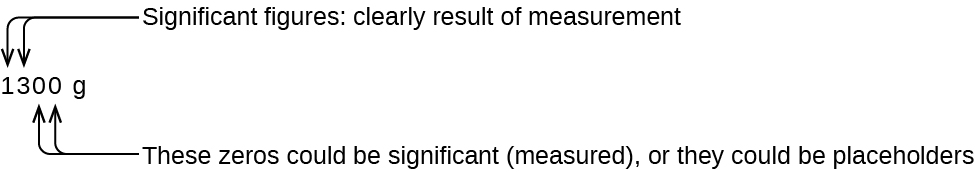
When determining pregnant figures, be sure to pay attention to reported values and think about the measurement and significant figures in terms of what is reasonable or probable—that is, whether the value makes sense. For example, the official January 2014 census reported the resident population of the US as 317,297,725. Do you recollect the Usa population was correctly determined to the reported nine significant figures, that is, to the verbal number of people? People are constantly being born, dying, or moving into or out of the country, and assumptions are made to account for the large number of people who are not actually counted. Because of these uncertainties, it might be more reasonable to look that we know the population to within maybe a 1000000 or so, in which example the population should be reported equally 317 million, or \(3.17 \times 10^viii \) people.

Meaning Figures in Calculations

A second important principle of dubiousness is that results calculated from a measurement are at least as uncertain as the measurement itself. We must take the uncertainty in our measurements into account to avoid misrepresenting the dubiousness in calculated results. One manner to do this is to written report the result of a adding with the correct number of meaning figures, which is determined by the post-obit 3 rules for rounding numbers:

1. When we add together or subtract numbers, nosotros should round the upshot to the same number of decimal places equally the number with the least number of decimal places (the least precise value in terms of add-on and subtraction).
2. When we multiply or divide numbers, we should circular the event to the same number of digits as the number with the least number of pregnant figures (the to the lowest degree precise value in terms of multiplication and partition).
3. If the digit to be dropped (the one immediately to the right of the digit to be retained) is less than v, we "round down" and leave the retained digit unchanged; if it is more than 5, nosotros "round upward" and increase the retained digit past 1; if the dropped digit is 5, we round up or down, whichever yields an even value for the retained digit. (The terminal function of this rule may strike you as a bit odd, but it'south based on reliable statistics and is aimed at avoiding whatever bias when dropping the digit "five," since it is equally close to both possible values of the retained digit.)

The following examples illustrate the application of this dominion in rounding a few dissimilar numbers to three significant figures:

• 0.028675 rounds "upwardly" to 0.0287 (the dropped digit, 7, is greater than v)
• xviii.3384 rounds "down" to xviii.3 (the dropped digit, three, is less than 5)
• six.8752 rounds "up" to 6.88 (the dropped digit is 5, and the retained digit is even)
• 92.85 rounds "down" to 92.8 (the dropped digit is 5, and the retained digit is even)

Let'due south work through these rules with a few examples.

Example \(\PageIndex{1}\): Rounding Numbers

Round the following to the indicated number of significant figures:

1. 31.57 (to two significant figures)
2. 8.1649 (to 3 significant figures)
3. 0.051065 (to iv significant figures)
4. 0.90275 (to iv significant figures)

Solution

1. 31.57 rounds "up" to 32 (the dropped digit is 5, and the retained digit is even)
2. 8.1649 rounds "down" to 8.16 (the dropped digit, four, is less than 5)
3. 0.051065 rounds "downwardly" to 0.05106 (the dropped digit is 5, and the retained digit is even)
4. 0.90275 rounds "upwards" to 0.9028 (the dropped digit is five, and the retained digit is even)

Exercise \(\PageIndex{ane}\)

Round the following to the indicated number of pregnant figures:

1. 0.424 (to two pregnant figures)
2. 0.0038661 (to three pregnant figures)
3. 421.25 (to four pregnant figures)
4. 28,683.five (to v meaning figures)

Answer a

0.42

Reply b

0.00387

Answer c

421.2

Answer d

28,684

Example \(\PageIndex{2}\): Addition and Subtraction with Significant Figures Dominion:

When we add or decrease numbers, we should round the result to the same number of decimal places as the number with the least number of decimal places (i.e., the least precise value in terms of addition and subtraction).

1. Add 1.0023 thousand and 4.383 g.
2. Subtract 421.23 k from 486 g.

Solution

(a)

\[\begin{align*}
&\mathrm{1.0023\: g}\\ +\: &\underline{\mathrm{4.383\: one thousand}\:\:}\\ &\mathrm{5.3853\: g}
\cease{align*}\]

Answer is 5.385 one thousand (round to the thousandths place; three decimal places)

(b)

\[\brainstorm{align*}
&\mathrm{486\: m}\\ -\: &\underline{\mathrm{421.23\: g}}\\ &\mathrm{\:\:64.77\: g}
\end{align*}\]

Answer is 65 one thousand (circular to the ones place; no decimal places)

Practice \(\PageIndex{2}\)

1. Add 2.334 mL and 0.31 mL.
2. Subtract 55.8752 m from 56.533 m.

Answer a

2.64 mL

Answer b

0.658 one thousand

Example \(\PageIndex{three}\): Multiplication and Partitioning with Significant Figures

Dominion: When we multiply or divide numbers, nosotros should circular the result to the same number of digits as the number with the least number of pregnant figures (the least precise value in terms of multiplication and segmentation).

1. Multiply 0.6238 cm by 6.half-dozen cm.
2. Divide 421.23 1000 by 486 mL.

Solution

(a)

\[\mathrm{0.6238\: cm\times6.half dozen\:cm=iv.11708\:cm^2\rightarrow issue\: is\:4.1\:cm^2}\:\textrm{(round to two significant figures)}\]
\[\textrm{4 meaning figures}\times \textrm{two significant figures}\rightarrow \textrm{two significant figures respond}\]

(b)

\[\mathrm{\dfrac{421.23\: g}{486\: mL}=0.86728...\: m/mL\rightarrow result\: is\: 0.867\: g/mL} \: \textrm{(round to three meaning figures)}\]

\[\mathrm{\dfrac{5\: pregnant\: figures}{three\: meaning\: figures}\rightarrow three\: significant\: figures\: answer}\]

Exercise \(\PageIndex{iii}\)

1. Multiply 2.334 cm and 0.320 cm.
2. Divide 55.8752 m past 56.53 due south.

Answer a

0.747 cm²

Answer b

0.9884 m/southward

In the midst of all these technicalities, it is important to proceed in listen the reason why we use meaning figures and rounding rules—to correctly correspond the certainty of the values we written report and to ensure that a calculated result is not represented as existence more than certain than the least certain value used in the adding.

Instance \(\PageIndex{four}\): Calculation with Significant Figures

One common bathtub is 13.44 dm long, v.920 dm wide, and 2.54 dm deep. Assume that the tub is rectangular and calculate its approximate volume in liters.

Solution

\[\begin{marshal*}
V&=50\times w\times d\\ &=\mathrm{13.44\: dm\times five.920\: dm\times 2.54\: dm}\\ &=\mathrm{202.09459...dm^3}\:\textrm{(value from estimator)}\\ &=\mathrm{202\: dm^three,}\textrm{ or 202 L (answer rounded to three significant figures)}
\finish{align*}\]

Practise \(\PageIndex{iv}\): Conclusion of Density Using H2o Deportation

What is the density of a liquid with a mass of 31.1415 m and a volume of 30.xiii cm³?

Answer

1.034 grand/mL

Example \(\PageIndex{four}\)

A piece of rebar is weighed and then submerged in a graduated cylinder partially filled with water, with results as shown.

1. Use these values to determine the density of this piece of rebar.
2. Rebar is mostly iron. Does your result in (a) support this argument? How?

Solution

The volume of the piece of rebar is equal to the book of the water displaced:

\[\mathrm{book=22.four\: mL-13.five\: mL=8.9\: mL=8.nine\: cm^3} \nonumber\]

(rounded to the nearest 0.one mL, per the rule for addition and subtraction)

The density is the mass-to-volume ratio:

\[\mathrm{density=\dfrac{mass}{volume}=\dfrac{69.658\: thou}{eight.ix\: cm^three}=7.8\: thousand/cm^3} \nonumber\]

(rounded to two meaning figures, per the rule for multiplication and partition)

The density of atomic number 26 is vii.9 thousand/cm^three, very close to that of rebar, which lends some support to the fact that rebar is by and large atomic number 26.

Do \(\PageIndex{four}\)

An irregularly shaped piece of a shiny yellow material is weighed and so submerged in a graduated cylinder, with results every bit shown.

1. Use these values to determine the density of this textile.
2. Practice you have whatever reasonable guesses as to the identity of this fabric? Explicate your reasoning.

Answer a

19 thou/cm^three

Answer b

It is likely gold; it has the right appearance for aureate and very close to the density given for gold.

Accurateness and Precision

Scientists typically make repeated measurements of a quantity to ensure the quality of their findings and to know both the precision and the accuracy of their results. Measurements are said to be precise if they yield very similar results when repeated in the same manner. A measurement is considered accurate if it yields a result that is very shut to the true or accepted value. Precise values agree with each other; accurate values agree with a true value. These characterizations tin be extended to other contexts, such equally the results of an archery contest (Figure \(\PageIndex{2}\)).

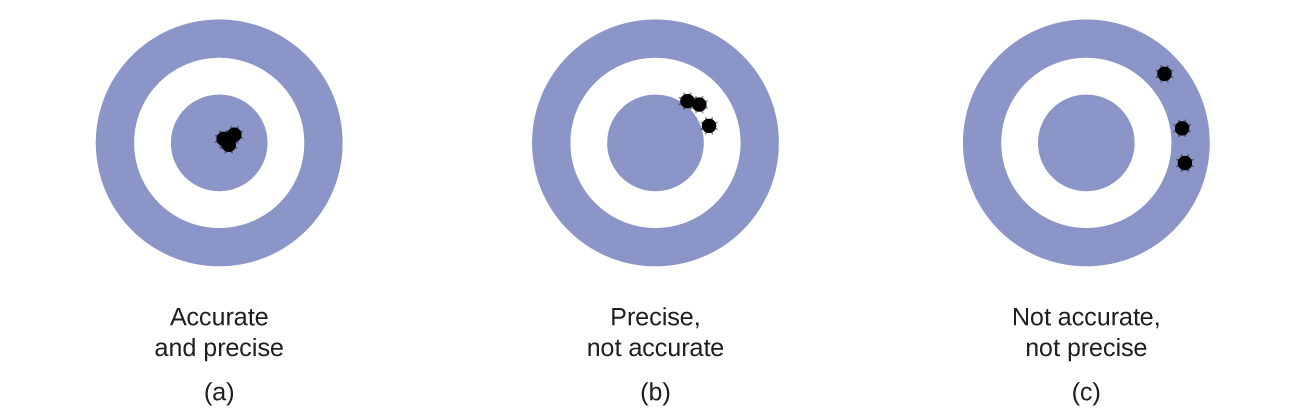
Figure \(\PageIndex{2}\): (a) These arrows are close to both the bull'due south middle and 1 another, so they are both accurate and precise. (b) These arrows are close to i some other simply not on target, and so they are precise but not accurate. (c) These arrows are neither on target nor close to one another, and so they are neither accurate nor precise.

Suppose a quality command chemist at a pharmaceutical visitor is tasked with checking the accuracy and precision of three unlike machines that are meant to dispense x ounces (296 mL) of cough syrup into storage bottles. She gain to apply each car to fill five bottles and then carefully determines the actual volume dispensed, obtaining the results tabulated in Table \(\PageIndex{2}\).

Table \(\PageIndex{2}\): Book (mL) of Coughing Medicine Delivered by 10-oz (296 mL) Dispensers

Dispenser #1	Dispenser #2	Dispenser #iii
283.3	298.iii	296.1
284.ane	294.2	295.9
283.9	296.0	296.1
284.0	297.viii	296.0
284.1	293.9	296.1

Considering these results, she will study that dispenser #1 is precise (values all close to one some other, within a few tenths of a milliliter) simply not authentic (none of the values are close to the target value of 296 mL, each being more than than 10 mL too low). Results for dispenser #2 represent improved accuracy (each volume is less than 3 mL away from 296 mL) merely worse precision (volumes vary by more than 4 mL). Finally, she tin report that dispenser #3 is working well, dispensing cough syrup both accurately (all volumes within 0.1 mL of the target book) and precisely (volumes differing from each other by no more than 0.2 mL).

Summary

Quantities can be exact or measured. Measured quantities accept an associated uncertainty that is represented by the number of meaning figures in the measurement. The dubiousness of a calculated value depends on the uncertainties in the values used in the calculation and is reflected in how the value is rounded. Measured values tin can be accurate (close to the true value) and/or precise (showing little variation when measured repeatedly).

Glossary

uncertainty

estimate of amount by which measurement differs from true value

pregnant figures

(also, significant digits) all of the measured digits in a conclusion, including the uncertain last digit

rounding

process used to ensure that calculated results properly reflect the uncertainty in the measurements used in the calculation

precision

how closely a measurement matches the same measurement when repeated

exact number

number derived past counting or by definition

accurateness

how closely a measurement aligns with a correct value

10 Ml Graduated Cylinder Uncertainty,

Source: https://chem.libretexts.org/Courses/University_of_Kentucky/UK:_General_Chemistry/01:_Essential_Ideas/1.5:_Measurement_Uncertainty_Accuracy_and_Precision

Posted by: ortegaandutimmose.blogspot.com

Share this post