Simplifying Square Roots

To simplify a foursquare root: make the number within the square root every bit small as possible (but still a whole number):

Instance: √12 is simpler equally two√3

Get your estimator and check if you want: they are both the same value!

Here is the rule: when a and b are not negative

√(ab) = √a × √b

And hither is how to use it:

Instance: simplify √12

12 is 4 times iii:

√12 = √(four × 3)

Utilise the rule:

√(4 × 3) = √4 × √3

And the square root of 4 is two:

√four × √3 = two√three

So √12 is simpler as 2√iii

Another example:

Example: simplify √8

√8 = √(4×2) = √4 × √two = 2√2

(Because the foursquare root of 4 is 2)

And another:

Case: simplify √eighteen

√18 = √(9 × 2) = √9 × √2 = 3√2

It frequently helps to cistron the numbers (into prime numbers is best):

Example: simplify √6 × √15

Commencement we can combine the ii numbers:

√6 × √15 = √(six × xv)

And then we factor them:

√(6 × xv) = √(2 × 3 × 3 × 5)

Then we see ii 3s, and make up one's mind to "pull them out":

√(2 × 3 × 3 × 5) = √(3 × 3) × √(2 × 5) = three√10

Fractions

There is a like dominion for fractions:

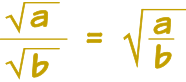
root a / root b = root (a / b)

Instance: simplify √30 / √x

Beginning we tin can combine the 2 numbers:

√thirty / √10 = √(xxx / ten)

And so simplify:

√(30 / 10) = √3

Some Harder Examples

Example: simplify √20 × √five √ii

Meet if y'all can follow the steps:

√20 × √5 √ii

√(two × two × 5) × √v √2

√ii × √2 × √v × √5 √two

√ii × √5 × √5

√2 × 5

5√two

Example: simplify 2√12 + 9√3

Beginning simplify 2√12:

2√12 = 2 × 2√3 = four√iii

At present both terms have √3, we can add together them:

4√3 + 9√iii = (four+9)√3 = 13√iii

Surds

Annotation: a root we can't simplify further is chosen a Surd. So √3 is a surd. But √4 = ii is not a surd.